Asynchronous PDE Solvers
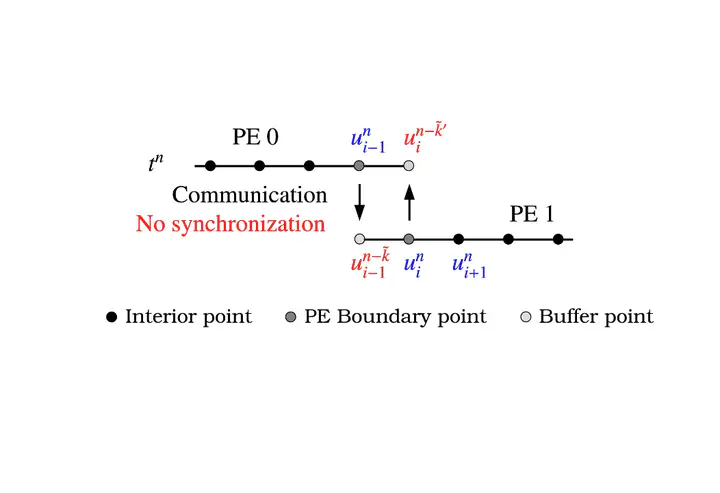
Designing scalable CFD codes on massively parallel computers is a challenge. This is mainly due to the large number of communications between processing elements (PEs) and their synchronization, leading to idling of PEs. Indeed, communication will likely be the bottleneck in the scalability of codes on Exascale machines. Our recent work on asynchronous computing for PDEs based on finite-differences has shown that it is possible to relax synchronization between PEs at a mathematical level. Computations then proceed regardless of the status of communication, reducing the idle time of PEs and improving the scalability. However, accuracy of the schemes is greatly affected. We have proposed asynchrony-tolerant (AT) schemes to address this issue. In this work, we study the effect of asynchrony on the solution of fluid flow problems using standard and AT schemes. We show that asynchrony creates additional scales with low energy content. The specific wavenumbers affected can be shown to be due to two distinct effects: the randomness in the arrival of messages and the corresponding switching between schemes. Understanding these errors allow us to effectively control them, rendering the method’s feasibility in solving turbulent flows at realistic conditions on future computing systems.
Publications:
- Goswami, S.K. and Aditya, K., 2024. An asynchronous discontinuous Galerkin method for massively parallel PDE solvers. Computer Methods in Applied Mechanics and Engineering, 430, p.117218.
- Goswami, S.K., Matthew, V.J. and Aditya, K., 2023. Implementation of low-storage Runge-Kutta time integration schemes in scalable asynchronous partial differential equation solvers. Journal of Computational Physics, 477, p.111922.